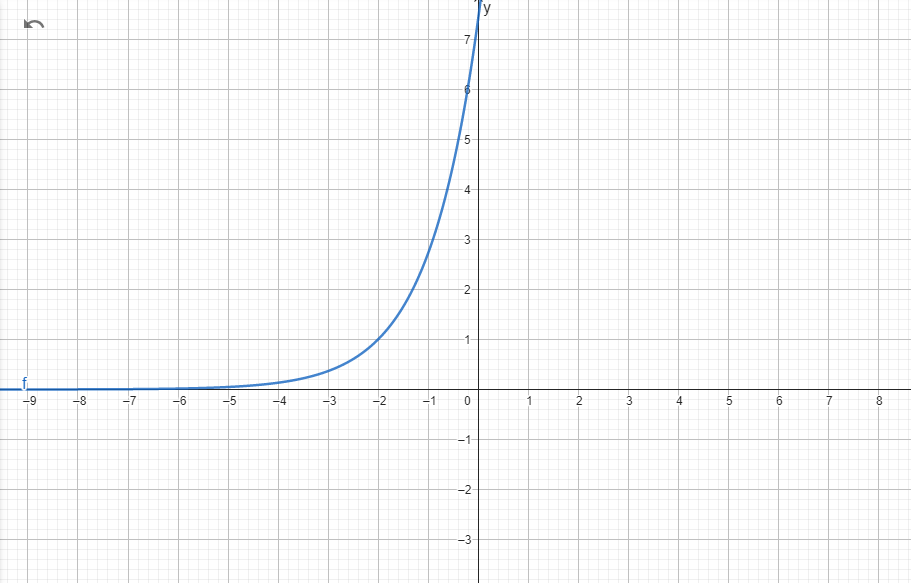
Función álgebraica (función lineal)

Está es una función es algebraica (función lineal) Su representación graficas es la siguiente: Figura:36 . Reprecenta la forma gráfica de la función "lineal " Ecuación:Y=3x-2 Dominio:(-∞,∞) Rango:(-∞,∞) Autora: Valencia González Joana